Introduction
Alpha
Beta
Standard Deviation
Sharpe Ratio
Sortino Ratio
Treynor Ratio
Information Ratio
Drawdown
Conclusion
Image of CVaR and Python code
1. Introduction
Imagine you're standing at the edge of a vast ocean, trying to predict the next wave. Now, imagine having a sophisticated set of tools that not only forecast the waves but also help you ride them with precision. That's the power of quantitative analysis in the financial markets. Just like a seasoned surfer reads the patterns of the ocean, investors armed with Alpha, Beta, and the Sharpe Ratio can navigate the ebbs and flows of the market with confidence. Join us as we dive deep into the world of quantitative analysis and unlock the secrets to making informed investment decisions.
2. Alpha
Imagine you expect your investment to grow by 8% over the next year. If your investment actually grows by 10%, then your Alpha would be positive, indicating that your investment performed better than expected. But if your investment only grows by 6%, then your Alpha would be negative, indicating that your investment didn't meet your expectations.
Alpha: In simple terms, alpha is like the score a fund manager gets for their investment performance. It tells us how well the manager has done compared to what we would expect given the level of risk taken. For example, if a fund has a positive alpha of 1%, it means the fund has outperformed its benchmark index by 1%. If it's negative, it means the fund has underperformed.
Jensen's Alpha: Now, Jensen's Alpha is like a supercharged version of alpha. It takes into account not just the overall performance of the fund, but also how much of that performance can be attributed to the skill of the fund manager rather than just the general movement of the market. It's named after Michael Jensen, the economist who developed the concept.
Jensen’s alpha is a measure of the excess return of a portfolio or security compared to what would be expected given its level of risk as measured by beta. It is used to evaluate the performance of an investment and can be calculated by subtracting the risk-free rate and the expected return based on the beta of the investment (the market risk premium) from the actual return of the investment.
For example, if the expected return of an investment with a beta of 1.5 (meaning it is expected to be 50% more volatile than the market) is 10% and the risk-free rate is 5%, the Jensen’s alpha for an investment with an actual return of 15% would be calculated as 15% — (5% + (1.5 * 5%)) = 5%. This would indicate that the investment has outperformed the expected return by 5% due to the manager’s skill or some other factor.
what is risk free rate?
The risk-free rate (RFR) is the theoretical rate of return on an investment with zero risk. It's a key component of modern finance and is the basis for many theories, including the capital asset pricing model (CAPM), modern portfolio theory (MPT), and the Black-Scholes model.
Think of it like this: imagine you have the option to invest your money in a completely risk-free asset, like a government bond. The interest rate you would earn on that investment is the risk-free rate. It serves as a benchmark for comparing the returns of other investments, which carry varying degrees of risk. Essentially, it's the minimum return an investor would expect for taking on additional risk with other investments.
3. Beta
Beta measures an investment’s sensitivity to market movements. It quantifies the extent to which an asset’s price fluctuates concerning the overall market. A beta greater than 1 implies higher volatility than the market, while a beta less than 1 suggests lower volatility.
Beta is like a teammate. It helps you see if your toy car is following the same path as your friend's toy car. If Beta is 1, it means your toy car is doing exactly the same as your friend's toy car. But if Beta is less than 1, it means your toy car is a bit different from your friend's toy car. And if Beta is more than 1, it means your toy car is very different from your friend's toy car.
Difference between Alpha and beta - ELI5
Alpha and Beta are like special helpers who help you understand how well your toy car is doing compared to your friend's toy car.
Alpha is like your personal cheerleader. It tells you how well your toy car is doing compared to what you expected. If your toy car goes faster than you thought it would, Alpha tells you that your car is doing a great job, even better than expected. But if it goes slower than expected, Alpha tells you that your car needs to try harder.
Beta is like a teammate. It helps you see if your toy car is following the same path as your friend's toy car. If Beta is 1, it means your toy car is doing exactly the same as your friend's toy car. But if Beta is less than 1, it means your toy car is a bit different from your friend's toy car. And if Beta is more than 1, it means your toy car is very different from your friend's toy car.
So, when you hear about Alpha and Beta in the stock market, just remember they're like your cheerleader and teammate, helping you understand how well your investments are doing compared to what you expected and how they're moving compared to the overall market.
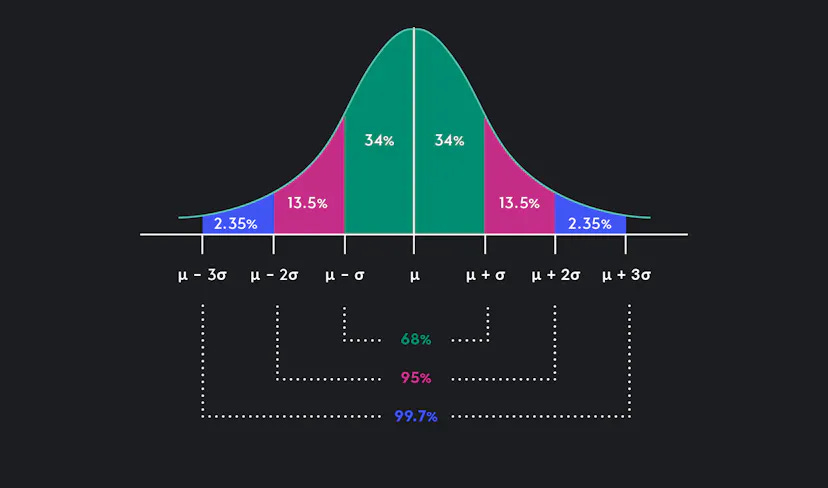
4. Standard Deviation
Standard deviation measures the dispersion of a dataset around its mean. In finance, it quantifies the volatility or variability of investment returns. Higher standard deviation indicates greater variability and higher risk.
Standard deviation is a way to measure how spread out or risky something is. In the stock market, it helps investors understand how much a stock's price might go up or down.Think of it like this: imagine you have a bowl of marbles, and you want to know how far each marble is from the average. The standard deviation tells you how spread out the marbles are from the middle.
For example, let's say you have two stocks, Stock A and Stock B. Stock A has a standard deviation of 1, which means its price doesn't change much. Stock B has a standard deviation of 3, which means its price can change a lot.
Now, let's say you have $100 to invest. You might want to put more money in Stock A because it's less risky, even though it might not have as high of a potential return as Stock B.
One verifiable fact is that standard deviation is a commonly used measure of risk in the stock market. It helps investors make informed decisions about where to put their money.
ELI5 - Explain Like I Am 5 Yrs. Old
Alright, let's imagine you have a box of your favorite candies, and you really like to eat them every day. Sometimes, you notice that the number of candies you get each day is different. Some days you get a lot, and some days you get fewer.
Now, let's say you keep track of how many candies you get each day for a month. If you look at these numbers, you might notice that they're all over the place. Some days you get 10 candies, some days you get 15, and other days you might get only 5.
Standard deviation is like a way to measure how much these numbers change from day to day. If the standard deviation is small, it means that most days you get a similar number of candies, and there's not much variation. But if the standard deviation is big, it means that the number of candies you get each day can be very different, and there's a lot of variation.
So, in the stock market, standard deviation tells us how much the price of a stock changes from day to day. If the standard deviation is small, it means the price doesn't change much, but if it's big, it means the price can change a lot. It helps us understand how risky a stock might be.
5. Sharpe Ratio
The Sharpe ratio is a measure of risk-adjusted return, which compares the expected return of an investment to the level of risk taken on to achieve that return. It is calculated by dividing the excess return (the return of the investment over the risk-free rate) by the standard deviation of returns.
Sharpe Ratio = (Return — Risk-Free Rate) / Standard Deviation
For example, let’s say an investor has a portfolio with an annual return of 10% and the risk-free rate is 3%. The excess return is therefore 10% — 3% = 7%. If the standard deviation of returns for the portfolio is 4%, then the Sharpe ratio is 7% / 4% = 1.75.
A higher Sharpe ratio indicates that the investor is receiving a higher return for the level of risk taken on, and a lower Sharpe ratio indicates the opposite. So in this example, the investor is receiving a relatively high return for the level of risk taken on, as indicated by the Sharpe ratio of 1.75.
ELI5 - Explain Like I Am 5 Yrs. Old
Imagine you have two piggy banks where you save your money. One piggy bank is very safe but doesn't give you much money back, like putting your money in a jar at home. The other piggy bank is a bit riskier but gives you more money back, like investing your money in a toy that might become popular and valuable.
Example of sharpe ratio?
Now, the Sharpe ratio is like a special ruler that helps you decide which piggy bank is better for your money. It measures how much extra money you get back from the riskier piggy bank compared to the safe one. If the ruler shows a big number, it means the riskier piggy bank gives you a lot more extra money for the risk you take. But if the number is small, it means the extra money you get isn't worth the extra risk.
So, the Sharpe ratio helps you decide if it's better to keep your money in a safe place or take a little more risk to get more money back.
Let's say you have two investment options: Option A and Option B.
Option A: It has an expected return of 8% with a standard deviation (a measure of risk) of 10%.
Option B: It has an expected return of 6% with a standard deviation of 5%.
Now, let's calculate the Sharpe Ratio for each option.
For Option A:
Expected Return: 8%
Risk-Free Rate: Let's assume it's 2%.
Standard Deviation: 10%
Sharpe Ratio for Option A = (8% - 2%) / 10% = 0.6
For Option B:
Expected Return: 6%
Risk-Free Rate: Let's assume it's 2%.
Standard Deviation: 5%
Sharpe Ratio for Option B = (6% - 2%) / 5% = 0.8
Comparing the two options, Option B has a higher Sharpe Ratio (0.8) compared to Option A (0.6). This indicates that Option B provides a better risk-adjusted return, meaning it gives you more return for each unit of risk you take compared to Option A. So, according to the Sharpe Ratio, Option B would be the preferable investment.
6. Sortino Ratio
The Sortino ratio is a risk-adjusted measure of return that was developed to overcome the limitations of the Sharpe ratio. Like the Sharpe ratio, the Sortino ratio is used to evaluate the performance of an investment by comparing the return earned to the risk taken. However, unlike the Sharpe ratio, which measures risk based on the standard deviation of returns, the Sortino ratio measures risk based on the standard deviation of negative returns (also known as downside risk).
Sortino Ratio = (Return — Target Return) / Downside Deviation
ELI5 - Explain Like I Am 5 Yrs. Old
Alright, imagine you have a piggy bank where you keep your money. Every day, you put some money into your piggy bank, hoping to save up more over time. But here's the thing: sometimes, you might lose some of the money you've saved.
Now, let's say you have two piggy banks: Piggy Bank A and Piggy Bank B.
With Piggy Bank A, you notice that some days you lose a little bit of money, but other days you gain a lot. On average, you're saving more money over time, but there's a chance you might lose some along the way.
With Piggy Bank B, you also notice that some days you lose money, but it's not as much as Piggy Bank A. So, while you're not saving as much on average compared to Piggy Bank A, you feel safer because you're not losing as much money on bad days.
The Sortino Ratio is like a measurement of how well your piggy bank is doing, but it focuses on how much you lose on bad days rather than just looking at the overall average. It tells you if the extra money you're saving in Piggy Bank A is worth the risk of losing more money on bad days.
For example, if Piggy Bank A has a higher Sortino Ratio than Piggy Bank B, it means that even though you might lose more money on some days, you're still saving more overall and the risk might be worth it. But if Piggy Bank B has a higher Sortino Ratio, it means you're not saving as much, but you're also not risking as much, so it might be a safer option for you.
How to calculate it?
To calculate the Sortino ratio, you need to first calculate the excess return, which is the difference between the investment’s return and the risk-free rate of return. You then divide this excess return by the downside standard deviation, which is calculated using only the negative returns of the investment.
For example, let’s say you have a portfolio that has earned a return of 10% over the past year. The risk-free rate of return for the same period was 2%, so the excess return for the portfolio is 8%. The downside standard deviation for the portfolio was 3%, so the Sortino ratio for the portfolio would be 8% / 3% = 2.67.
This indicates that the portfolio has earned an excess return of 2.67 times the downside risk taken. A higher Sortino ratio is generally considered to be more desirable, as it indicates that the investment has generated a higher return for a given level of risk.
What is risk adjusted return?
Risk-adjusted return is a measure used to assess the performance of an investment by considering the amount of risk taken to achieve that return. It helps investors evaluate whether the return generated by an investment adequately compensates for the level of risk involved.
In simple terms, it's like comparing two investments that offer the same return but have different levels of risk. The one with lower risk would generally be considered to have a better risk-adjusted return because it achieves the same return with less risk.
For example, if Investment A provides a return of 8% with a standard deviation (a measure of risk) of 10%, and Investment B provides the same 8% return with a standard deviation of only 5%, then Investment B would be considered to have a better risk-adjusted return because it achieves the same return with less risk.
Difference between sharpe and sortino ratio
The Sharpe ratio and Sortino ratio are both popular tools used in finance to measure the risk-adjusted return of an investment. The Sharpe ratio, developed by Nobel laureate William F. Sharpe, calculates the excess return of an investment (return above the risk-free rate) per unit of its volatility. The formula for the Sharpe ratio is (Return of Investment - Risk-Free Rate) / Standard Deviation of Investment. A higher Sharpe ratio indicates a better risk-adjusted return.
On the other hand, the Sortino ratio, named after Frank A. Sortino, focuses on the downside risk of an investment by only considering the volatility of returns below a certain threshold (usually the risk-free rate or a target return). The formula for the Sortino ratio is (Return of Investment - Risk-Free Rate) / Downside Deviation of Investment. The Sortino ratio penalizes the investment for volatility in returns below the threshold, as it considers only the downside risk in its calculation.
To illustrate the difference between the two ratios, let's consider an investment with an annual return of 10%, a standard deviation of 15%, and a downside deviation of 10%. If the risk-free rate is 2%, the Sharpe ratio would be (10% - 2%) / 15% = 0.53, while the Sortino ratio would be (10% - 2%) / 10% = 0.8. In this case, the Sortino ratio gives a higher value, indicating that the investment has a better risk-adjusted return when considering only downside risk.
A verifiable fact is that the Sharpe ratio is widely used in the finance industry to evaluate the performance of investment portfolios, while the Sortino ratio is preferred by some investors who are more concerned with minimizing downside risk.
7. Treynor Ratio
The Treynor ratio is a measure of risk-adjusted return. It is calculated by dividing the portfolio’s excess return over the risk-free rate by the portfolio’s beta.
Treynor Ratio = (Return — Risk-Free Rate) / Beta
For example, suppose a portfolio has a return of 10% over the risk-free rate of 5% and a beta of 1.5. The Treynor ratio for this portfolio would be (10% — 5%) / 1.5 = 3.33%. This means that for every 1% increase in the market’s return, the portfolio’s return is expected to increase by 3.33%.
The Treynor ratio is a measure used to assess the risk-adjusted return of an investment or a portfolio. It's similar to the Sharpe ratio but instead of using total risk (standard deviation) in the denominator, it uses systematic risk, often measured by beta.
In simple terms, the Treynor ratio compares the excess return of an investment (or portfolio) over the risk-free rate to the investment's systematic risk. It helps investors evaluate whether the excess return earned by an investment adequately compensates for the systematic risk taken.
The formula for the Treynor ratio is:
For example, if an investment has an expected return of 10%, the risk-free rate is 3%, and the beta is 1.2, then the Treynor ratio would be calculated as:
This means that for each unit of systematic risk (measured by beta), the investment earns approximately a 5.83% excess return above the risk-free rate.
ELI5 - Explain Like I Am 5 Yrs. Old
Alright, imagine you have a bunch of toys, and you want to share them with your friends. But some toys are more special and might get lost or broken more easily, while others are more sturdy. Now, let's pretend you have a magic number that tells you how much each toy gets broken or lost when you play with it.
The Treynor ratio is like counting how many toys you can share with your friends compared to how easily they get lost or broken. If you can share a lot of toys without many of them getting lost or broken (low risk), that's good! But if you can only share a few toys and they often get lost or broken (high risk), that's not so good.
So, the Treynor ratio helps us figure out if sharing our toys (investments) is worth it compared to how likely they are to get lost or broken (the risk). If it's a high number, it means we're getting a lot of toys for the risk we're taking, which is good! If it's a low number, it means we're not getting many toys for the risk, which is not so good.
8. Information ratio
The information ratio is a measure of the excess return of an investment portfolio compared to a benchmark index, per unit of risk taken. It is calculated as the portfolio’s excess return (the difference between the portfolio’s return and the benchmark’s return) divided by the portfolio’s standard deviation, which is a measure of the portfolio’s risk. A higher information ratio indicates that the portfolio is generating higher excess returns per unit of risk taken, compared to the benchmark.
Information Ratio = Excess Return / Tracking Error
For example, consider an investment portfolio that has a return of 10% over the past year, and a benchmark index that has a return of 8%. The excess return of the portfolio is 2%. If the portfolio’s standard deviation is 4%, then the information ratio is 2% / 4% = 0.5. This means that the portfolio is generating 0.5 units of excess return per unit of risk taken, compared to the benchmark.
On the other hand, if the portfolio has a higher standard deviation of 6%, then the information ratio would be 2% / 6% = 0.33. This means that the portfolio is generating lower excess returns per unit of risk taken, compared to the benchmark.
9. Drawdown
The drawdown is a measure of the maximum loss an investment or a trading strategy has experienced over a given period of time. It is calculated as the difference between the peak value and the lowest subsequent value, expressed as a percentage of the peak value. For example, if an investment starts with a value of $100 and reaches a peak of $120, but then drops to a low of $80, the drawdown would be calculated as (120–80)/120 = 33.3%. This means that the investment has lost 33.3% of its value from its peak.
Imagine you have a piggy bank where you save your pocket money. Sometimes, instead of adding more money to your piggy bank, you might end up taking some money out. Drawdown in the stock market is similar. It refers to the amount of money you lose from the highest point your investment portfolio has reached to the lowest point it reaches before starting to increase again.
For example, let's say you invest $100 in the stock market, and after a while, the value of your investment grows to $150. But then, the market takes a downturn, and the value of your investment drops to $120. The drawdown in this case would be $30 ($150 - $120), representing the decrease in value from the highest point to the lowest point before it starts to recover. It's like the money you took out of your piggy bank, but in this case, it's the decrease in your investment value.
Conlusion:
In summary, these metrics offer valuable insights into the risk and return characteristics of investments. By considering alpha, beta, Sharpe Ratio, Sortino Ratio, Treynor Ratio, and drawdowns together, investors can make more informed decisions, construct well-diversified portfolios, and manage risk effectively in both investment and trading activities.
Next upcoming post will be on python code to implement the quantitative ratios and risk management:
Thank you for reading! I hope you enjoyed it. Please feel free to comment below to discuss anything further, and we can connect. I'm currently working on developing a Technical and Quantitative analysis tool for the Indian market, and I would greatly appreciate your help in building it. Thanks again!